Imagem de capa: Cesto de palha. Imagem de lifeforstock no Freepik.
FOBIA DE MATEMÁTICA, ENSINO DE MATEMÁTICA E O MUNDO COMO UM CENTRO DE CIÊNCIAS
Maurice Jacques Bazin – (1934-2009)
Este documento foi compartilhado na sessão “Math Phobia and Science Centers: Some International Perspectives” (A Fobia Matemática e os Centros de Ciências: Algumas Perspectivas Internacionais) na Conferência 2004 da Association of Science-Technology Centers (ASTC) em San Jose, Califórnia.
Obs.: Atualmente é mais comum o uso do termo Math Anxiety – Ansiedade Matemática – em pesquisas sobre o medo da Matemática que pode variar de uma não identificação pessoal com a matemática à uma fobia extrema com conhecimentos matemáticos. Em grande parte, ela é decorrente de processos educacionais.
Crescer sem Medo da Matemática
Escrevo para todos vocês, colegas professores, hoje, de dentro da Floresta Amazônica. Mas, cresci francês, em Paris. Eu tinha quinze anos quando entrei pela primeira vez em uma biblioteca . As bibliotecas públicas não eram comuns na época [1949].
Minha mãe, que conhecia um bibliotecário, me apresentou a Biblioteca da Academia Francesa. Sem saber para que estava ali, pedi o primeiro livro de Descartes. Acho que minha escolha veio de ter aprendido “coordenadas cartesianas” e ouvido falar sobre “O Método” e de ter ficado intrigado com a lógica de dizer “penso, logo existo”. Eu ia conhecer de alguma forma o ser humano cujo nome se ligava àquelas coisas. Consegui a primeira edição. Talvez eu tivesse em minhas mãos o próprio livro que ele apresentou à Academia.
Folheei e parei em seus desenhos de raios de luz passando por gotas em um arco-íris. Esses desenhos eram tentativas de representar algo que Descartes estava tentando entender; era o seu processo de pensamento original do qual eu estava me aproximando. Enquanto eu lia o que ele colocava em palavras e decifrava seus rabiscos, eu o acompanhava e recriava tudo para mim.
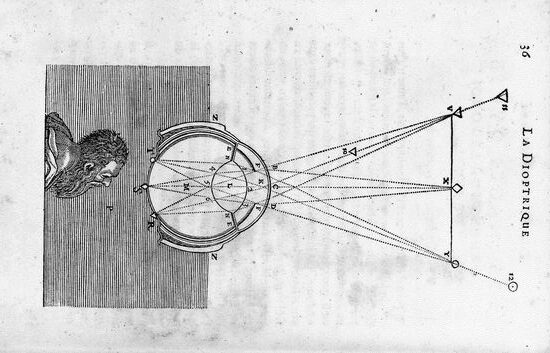
Muitos anos depois, em outra biblioteca especial, a Library Tower em Yale [Biblioteca Memorial Sterling], me deparei com um texto de Voltaire [François-Marie Arouet (1694-1778) escritor, historiador e filósofo iluminista francês] descrevendo como ele e sua amante [Gabrielle Émilie Le Tonnelier de Breteuil, marquesa de Châtelet-Laumont, (1706-1749) cientista nos campos da física e da matemática] estavam pesando barras de ferro quando esquentavam até ficarem brancas quentes, e quando frias, tentando encontrar uma diferença.
Eu já havia coescrito o livro Introdução à Relatividade Geral até então, e gostaria de ter colocado nele, a tentativa de Voltaire de pesar energia no século 18, fazendo de verdade um dos experimentos mentais de Einstein!
O ponto dessa reflexão é que esse aprendizado contínuo que vivi não foi formal, embora tenha acontecido em lugares mais formais. Era simplesmente estar em contato com realidades criadas por outros, com investigações originais contadas por seus próprios autores, situações que satisfaziam minha própria curiosidade normal, assim como Júlio Verne satisfazia minha imaginação além dessas realidades. Além disso, todo esse aprendizado difuso ocorreu dentro da minha cultura nativa, em minha língua materna.
Então, nunca passou pela minha cabeça francesa ter medo de coisas de aparência teórica ou matemática. Meu próprio remédio contra o tédio de fazer exercícios formais de matemática bastante repetitivos na pós-graduação em francês era encontrar soluções geométricas para problemas algébricos, entrando em competição criativa, gritando soluções “elegantes” dos bancos de madeira do Lycée Saint Louis, com o agora matemático francês Adrien Douady (1935-2006) [Douady é consultor matemático da série Dimensions… une promenade mathématique que apresenta a história do conceito de dimensão, disponível em português]. De alguma forma, nunca tivemos medo da matemática.
Nossa cultura francesa exala organização, formalidade e lógica. Nossa própria linguagem exige uma sistematização precisa, única, correção em tudo, do sotaque à ortografia. Há regras rígidas na gramática e de modos à mesa. “É assim, porque é assim”, disse minha avó quando não encontrou argumentos em uma discussão comigo quando criança. Assim, as crianças francesas estão mais familiarizadas com as formalizações culturais gerais e, portanto, entram nas formalidades da “matemática na escola” sem estranhamento.
A Origem do Medo
Parece-me que pode haver algo especificamente “anglo” nesse caso do “medo da matemática”. Isso pode parecer ridículo no início, já que a Inglaterra tinha Newton, enquanto a França tinha Descartes. Mas há uma diferença séria: enquanto Descartes escrevia tudo em francês, Newton tinha que escrever suas coisas matemáticas/teóricas em latim (você sabe, para a sobrevivência política em um mundo dominado pela Igreja; ele tinha que obedecer às suas leis, e ele tinha medo de seu poder).
Então, o trabalho matemático de Newton nasceu distante de todos, quero dizer, de pessoas como você e eu daquela época. E hoje, no mundo anglo global, a Matemática ainda é majoritariamente para pessoas ligadas a um ou outro, colonizador ou colonizado. Por outro lado, Newton escreveu sobre o mundo físico experimental na língua de todos, o inglês, e não o latim, em seus livros sobre “Óptica”. Talvez isso se reflita no fato de que os educadores de língua inglesa não têm tanto “medo da física” quanto da matemática. A abordagem tipicamente “empírica” norte-americana dos problemas físicos não se estende aos problemas de matemática.
E respiramos essa diferença em nossas salas de aula. Lá, o aspecto puramente formal da matemática domina nossas vidas. Os principais formalizadores não estão fisicamente presentes, mas governam-nos a todos: são os “Autores de Manuais Escolares”. Eles nos imprimem a formalidade do processo de escolarização. Não são “autores” no sentido que Descartes ou Newton foram. Eles definem e dominam nossos caminhos de ensino. São filhos e filhas, intelectualmente, isto é, de escritores de livros didáticos anteriores; e, às vezes, essa tendência ocorre em uma família que entrou no comércio dentro da produção controlada pelo Estado. No Brasil, existem linhagens de autores de livros didáticos, um banco de dados de indivíduos “reconhecidos” pelo Ministério da Educação. E hoje, eles raramente se desviam da abordagem ditada pelos EUA para o maneirismo padrão dos livros didáticos. O mundo inteiro ainda sofre com os desenhos com círculos que se cruzam e que afirmam apresentar “conjuntos”, um exemplo de inveja básica da abstração francesa, reduzida e falsificada em “nova” matemática por contadores de feijão submissos e técnicos de escrita de livros didáticos em todo o mundo.
Hoje, nada de matemático é vivido diretamente, verdadeiramente, dentro dos desejos e necessidades de cada um, em todo o mundo. A não ser dentro de alguns cantos aborígenes ou indígenas da humanidade, em pequenas rachaduras no que ainda chamarei, como em maio de 1968, de “Sistema”.
Dor Matemática
E vou compartilhar com vocês em um minuto minha própria experiência dentro de uma dessas aberturas indígenas para a matemática viva. Mas, no geral, estamos testemunhando a concentração de poder em uma elite que se define como educadores de livros didáticos, cada geração mais formalista que a anterior, cada geração apenas reorganizando as formalidades concebidas pela anterior; produzem manuais sempre organizados por série, apresentando conceitos supostamente adequados à série (como se eu optasse por ler Descartes em termos da série em que eu estava na época!), apresentando sucessões de tópicos, criando regras e sequências pedagógicas, “piagetizando’ currículos.
Fingem que a aprendizagem é logicamente sequencial, linearizam-nos a todos; e os professores, por sua vez, colocam as crianças na fila, exercício após exercício, capítulo após capítulo. Os escritores de livros didáticos e os autodenominados Professores de Educação, com P e E maiúsculos, perpetuam a estrutura de perfuração; são os “sargentos” que latem no campo de treinamento educacional chamado escolarização.
A matemática escolar é simplesmente uma dor.
[Pesquisas da Universidade de Chicago da psicóloga cognitiva Sian Beilock, com estudos em neurociência demonstram que a região cerebral de dor física é ativada por estudantes que sofrem de ansiedade matemática, ou seja, quando as pessoas sentem fobia de matemática, o cérebro sente dor].
Através do acompanhamento oficial de livros, a Matemática tornou-se associada a colocar coisas, e pensamentos, em caixas categóricas. E o ensino consiste na abertura de uma série de caixas, seguindo um caminho através de uma grade curricular. Devemos viajar por sequências de tópicos hierarquicamente organizados, um feixe de títulos de capítulos e estes, à medida que o tempo traz novos rótulos da moda, são elevados a um status chamado referencial. Vivemos em uma metáfora de prisão.
Nosso problema é que não gostamos de viver ou aprender dentro de um quadro, dentro de fronteiras preestabelecidas. Não gostamos de ensinar quando se tem que executar um programa apenas para cumprir o programa, enchendo o cérebro das crianças até a borda. Quantidade pura, quantidades mensuráveis: estamos fazendo esse tipo de matemática o tempo todo; e estamos cansados disso, embora obedeçamos, como autômatos matemáticos.
Todas essas associações desagradáveis que acabam se transformando em medo, talvez às vezes em pânico e, então, uma vez empurradas de volta para o nosso subconsciente, reprimidas porque não queremos mais olha-las na cara, constroem uma fobia crônica… Isso é um substituto para a falta de desejos executáveis?
Não podemos viver só da quantidade:
- “Eu cobri esse tema?
- Terminei essa seção da última vez?
- Posso passar por cima dessa caixa nesta página?
- Posso atribuir essa parte como lição de casa?”
Estamos falando de mentes, falando matemática como uma linguagem administrativa “eduquês” em nossas próprias mentes. O modelo de plano de aula que devemos imaginar no café da manhã deve parecer uma série de caixas de cereais que esvaziaremos no quadro-negro, em linhas e colunas. Seguiremos uma matriz de apresentação e alguns de nós poderemos fazê-lo com Power Point. E, algum dia, teremos o “Power Line” para trabalhar.
Alguns autodenominados programadores educacionais prepararão tudo isso para nós; nós nos tornamos programáveis também.
Estamos sendo enganados, e nós e as crianças estamos certos em querer permanecer vivos, e não gostar nada disso!
Não é viva; é frígida, formalizada até a morte, a morte da curiosidade e da criatividade de todos. Estou brincando aqui com a linguagem da escola, porque brincar é viver; e isso me ajuda a ver o que está sendo dito e o que é impresso como ordens de ensino, em nome de uma organização supostamente necessária para que todos os professores entrem, degrau a degrau, subindo uma escada matemática de conhecimento universal.
De alguma forma, eu não precisava viver as coisas assim na França. A partir de certo ponto, geralmente nas séries superiores, cada professor insistia em dar o “seu” curso (todos os meus professores de matemática eram homens) e você tinha que tomar notas de sua própria autoria exposta na lousa. O aprendizado da matemática, então, era a partir da fala e da escrita reais de uma pessoa viva, não atrelado à formidável ordenação de um volume impresso.
Ao mesmo tempo, na minha juventude, as crianças argelinas cujos pais tentaram sobreviver econômica e fisicamente refugiando-se na França da guerra colonial em sua terra natal, só encontrariam (e esse “apenas” é fundamental) a matemática como material formal em livros didáticos rígidos, nunca na língua de suas mães.
Uma matemática indígena viva
É por isso que agora quero falar com vocês sobre esse assunto, pois o vejo de um canto específico do Terceiro Mundo, de muito longe da “barriga da besta” em que você vive. Mas, antes, deixe-me mostrar-lhe uma das minhas próprias “Belas Contradições (1969)” de que fala o poeta Nathaniel Tarn: devo confessar-vos que acabei de publicar um LIVRO DIDÁTICO de MATEMÁTICA!
[O poema The Beautiful Contradictions é um vórtice inspirador de mitologia, história e antropologia que leva a letra ao seu limite superior. Um vasto ecopoema para uma Terra agonizante, um poema socialmente radical, um drama matrilinear, uma iniciação judaico-maia-budista, um épico transatlântico que termina com uma chegada transamericana, um testamento que une ciência e imaginação].
“Demora muito tempo para trazer para a poesia
tudo o que cauteriza os espíritos de qualquer época em particular,
quando cada letra, cada palavra, cada vírgula, deve passar, cada respiração,
ser submetida a testes intermináveis,
então o que temos agora é a era da canção morta“.
Trecho de As Belas Contradições, Nathaniel Tarn, 1969.
O detalhe interessante sobre essa conquista é que eu não posso ler esse livro didático de matemática, e nenhum de vocês também poderia lê-lo; e pouquíssimas pessoas conseguiam reconhecer a notação matemática usada nele. [O livro é escrito em língua materna indígena].
O título que seus autores coletivos escolheram é: “Um guia para continuar investigando a maneira como nós ‘pessoas da cobra anaconda‘ contamos e medimos coisas”.
Eles, a quem chamamos de Tuyuka, não decidiram um nome para o que chamamos de matemática.
Eles precisam formalizar isso? Eles sabem o que fazem quando criam uma ordem para suas redes de pesca de acordo com o tamanho da malha (que eles produzem dando um nó em torno de ripas de madeira de lei padrão cujas larguras são medidas em dedos, ou seja, em larguras de dedos) e os tipos correspondentes de peixes que capturam e/ou não capturam. Há muita matemática, meus amigos, na elaboração do conteúdo por trás dessas frases!
Neste livro, você também encontra desenhos detalhados de abacaxis; as mulheres da comunidade ficaram muito felizes em investigar as famílias de linhagens que podem contar com os abacaxis que cultivam em suas roças de mandioca. Eles apresentaram suas descobertas a todos naquela casa que o homem branco basicamente os obrigou a construir e chamou de “escola”, mas que eles então se apropriaram, com uma pequena ajuda de seus conselheiros honestos, daqueles que estão trabalhando a serviço de sua cultura:
Primeiro, a antropóloga que não pensa mais em “se formar no mundo branco”, mas acompanha os professores indígenas em seu esforço de alfabetizar as crianças em sua língua materna (desculpem essas tecnicalidades, mas sem elas, eu estaria dando uma falsa impressão de simplicidade);
Em segundo lugar, o linguista que os ajudou a decidir como tornar sua língua mais viva, alfabetizar-se e donos da literatura, escrevendo-a primeiro, todos participando, escrevendo sem padronização ortográfica estrita: ler de volta não é difícil para quem conhece a língua; Pode parecer difícil para a pessoa branca que olha de fora e deseja regras rígidas, como se estivéssemos novamente fazendo algo onde apenas um caminho e uma resposta são permitidos, aquela coisa que seria como matemática de livro didático!
Terceiro, uma verdadeira matemática própria, que propôs que contar e medir era apenas parte de se expressar com partes especializadas da linguagem, com alguns símbolos como os que representam sons em palavras, dentro do modo de pensar a vida. Os povos indígenas Tuyuka organizaram os resultados, em sua língua, de suas linhas de contagem em abacaxis, discutiram, escolheram símbolos e notaram a regra que em nossa cultura branca chamamos de números de Fibonacci…
Parece-me estar muito longe do nosso tema medroso. E, no entanto, é a sua ausência [da fobia] na vida Tuyuka hoje que deve nos interessar aqui. Eles procuraram padrões no mundo ao seu redor e no mundo das ferramentas que foram desenvolvidas por seus ancestrais. Eles descobriram a matemática escondida em suas escolhas de padrões em cestos trançados que dormem no inconsciente dos tecelões. Descobriram sua etno-matemática, o que podemos chamar aqui de matemática de sua etnia, definida pela linguagem em que o grupo se expressa. E eles estão tão à vontade dentro dela quanto com sua “etno-religião”.
É divertido pesquisar a própria cultura em todos os seus aspectos, e fazer isso com as crianças, e chamá-la de aprendizagem e, talvez, para ser compreendida pelos escritores de livros didáticos, ensinando. Não foi nem assustador nem doloroso; essas ideias não se aplicavam. Nenhum de nós estava sendo perfurado em algo; e já não havia professores como “guardas prisionais”; essa expressão foi usada por um dos professores Tuyuka que foi obrigado a ensinar em português, pelos governantes brancos da educação colonizadora, para povos etnicamente diferentes, durante 30 anos. Ao descrever para seus colegas e para mim como acabara de ajudar um grupo de crianças a contar as folhas em espiral ao redor do caule de uma planta de mandioca, ele disse de repente: “Fui guarda prisional por 30 anos, mas agora vejo as crianças sendo felizes”. “Quando é que todos deixaremos de ser guardas prisionais?” Pergunto.
Museus / Escolas para aprendizes vivos
Alguém, há 35 anos, optou por fazer isso aqui mesmo na Califórnia, abrindo as portas do Palácio das Belas Artes sem qualquer inauguração formal do que se tornou o Exploratorium. E o que eu e os professores de Tuyuka fizemos juntos se assemelha muito concretamente ao que ainda fazemos, inspirados por Frank Oppenheimer, em nossos Centros de Ciências e Matemática: o lugar é cheio de coisas reais, materiais, coisas familiares aos visitantes ou estudantes que podem explorar e descobrir alguma organização, alguma ordem, algumas relações; ou maravilhar-se com alguma ordem explícita com a qual preparamos para brincar (como objetos simétricos ou desenhos que o visitante constrói e desconstrói, descobrindo a invariância e a variedade de regras de simetria).
Os Tuyuka fizeram exatamente isso com suas redes de pesca e suas técnicas de cestaria. Padrões em objetos tecidos exigem múltiplos para caber em um todo. A busca de regras na ramificação de plantas estranhamente regulares revelou o conceito de crescimento fractal. Mas tudo isso só fazia sentido para eles e fluía em suas interações e ensinamentos, porque fazíamos isso de dentro de sua cultura, de sua vida, de sua própria língua. E eles continuaram discutindo e encontrando alegria nessas descobertas, e compartilhando um pouco comigo em português quando paravam; e então eu podia às vezes dizer-lhes algo sobre como outras civilizações descobriram, brincaram e usaram tais conceitos.
Fiquei feliz, naquela época, por ter feito muita matemática multicultural com nossos colegas professores no Exploratorium nos anos 90. Dos “números do milho” da tecelã Kim Shuck de Tsalagi (poetisa, autora, tecelã e artista de miçangas da nação Cherokee), aos bancos de dados de Quipus incas, contei histórias do que aprendi com outras culturas. Os Tuyuka, então, escolheram a notação maia para representar seus números porque sua contagem, quando ouvida em sua língua, dá papéis especiais às unidades (o ponto maia), cinco (a barra maia) e 20 (a base maia e a escolha de posicionamento vertical). Aqui está uma fotografia de um cartaz feito por quatro crianças detalhando seu sistema de contagem e sua notação, enquanto contam peixes.
Poderia haver medos, ansiedades ou fobia nessa aventura intelectual? Há cinco anos, nenhum Tuyuka havia escrito uma palavra em sua língua. Seu processo de alfabetização é uma verdadeira alfabetização cultural, e é deles. Em nossos Centros de Ciências também fazemos alfabetização técnica e, quando nos permitimos pensar mais profundamente, fazemos e vivemos a alfabetização cultural em geral.
E ninguém tem medo.
O que correspondeu aos temores norte-americanos quando entrei pela primeira vez em território Tuyuka foi uma apreensão inicial adquirida através do “contato” com o mundo brasileiro. Na verdade, o raciocínio que me levou até lá em primeiro lugar foi bastante contorcido. No mundo oficial brasileiro da educação formal, a matemática é usada para selecionar pessoas, a técnica globalizada que consiste em avaliar e examinar e que todos nós somos obrigados a participar de nossas escolas.
A Educação Indígena, tal como imposta a partir do mundo político branco das Secretarias Estaduais ou Municipais de Educação, tenta reproduzir a técnica de escolarização desse homem branco. Mas alguns grupos indígenas, usando o reconhecimento pela Constituição brasileira de um direito indígena a uma educação “diferenciada” [em língua materna], e ajudados por indivíduos de ONGs dedicadas, conseguem definir sua própria maneira de fazer educação por meio de uma categoria recém-criada de indivíduos: professores indígenas, pagos pelo mundo branco oficial. Esses professores recém selecionados foram quase todos “educados” pelos vários tipos de missionários que invadiram a bacia amazônica em meados do século 20; nas escolas missionárias, eram proibidos de usar a própria língua e supostamente eram formados em Português, Matemática, Geografia, História com os mesmos livros, como qualquer criança brasileira.
Eles resistiram silenciosamente e dosaram tudo, nunca adquirindo as habilidades formais do homem branco. Hoje eles lembram e têm a chance de buscar alternativas. Mas eles nunca ouviram falar de outra coisa em matemática além das “quatro operações” e foi isso que me pediram para vir ensiná-los. Quando cheguei, pedi primeiro que me contassem sobre o seu contato com o aprendizado de matemática e todos confirmaram que “não aprenderam”. Eles tinham apenas “roçado”, então, sem doer e, portanto, eles não tinham tido tempo de se tornarem medrosos. Então, propus procurar suas próprias coisas da vida quando algumas repetições, regularidades ou alguma organização especial ocorressem. E partimos para a sua própria aventura na descoberta. Não se trata de medo, porque não havia dificuldades a priori, regras a seguir, abstrações necessárias. Não iríamos viver de formalidades, mas aproveitar a vida intelectual na descoberta da organização no mundo real, no mundo real.
Agora que eu disse tudo isso, eu entendo melhor por que criamos Centros de Ciência. Lembre-se por que Frank Oppenheimer criou o Exploratorium, para dar às pessoas comuns um verdadeiro acesso à alegria de descobrir, de exercitar sua capacidade intelectual por conta própria em meio a uma rica mistura de fenômenos naturais. E lembre-se que a maior conquista do Instituto de Professores no Exploratorium é fazer com que seus ex-estudantes não consigam dirigir rápido em nenhum momento, porque eles continuam encontrando coisas novas interessantes em seu campo de visão, e continuam observando, vendo e pensando como seres humanos, vivos, e não meros motoristas velozes de carros.
Nosso objetivo é desse porte. Somos a antítese do formalismo escolar, embora sejamos muito organizados na seriedade do que fazemos.
Oferecemos às pessoas algumas possibilidades de fazer, viver e sentir matemática, descobrindo que o conteúdo de matemática é encontrar padrões. (“Padrões” era a faixa original anunciando a área de exposições de matemática no Exploratorium). Os Centros de Ciências podem usar suas próprias palavras, criar categorias de atividades e inventar jogos sem se referir a grades, matrizes ou quadros de diretores. As pessoas reunidas aqui hoje são educadores de museus e professores de sala de aula que conhecem os centros de ciências e matemática e sabem a diferença entre o que pode acontecer lá e o que é aplicado em sala de aula. Minha proposta, então, para todos vocês, seria “não ter medo” e transformar sua sala de aula em um centro vivo de descoberta.
Lá será possível e prazeroso fazer matemática pesquisando o próprio mundo, como minha experiência com meus amigos Tuyuka me ensinou. Você desenvolve os conceitos que precisa à medida que eles aparecem e sabe o que eles têm a ver com o mundo real. Nossos filhos têm um mundo real em que vivem; E por mais politicamente incorreta que uma ida ao supermercado possa ser, ainda é uma maneira verdadeira de encontrar números de uso comum, combiná-los, ver como eles mudam, descobrir coisas reais sobre o que é economia. Tais atividades não criam medo da matemática.
Claudia Zaslavsky (1917-2006) propôs muitas atividades e estudos para as séries iniciais [alguns livros já trazudidos para português] e Marilyn Frankenstein para a educação matemática e etnomatemática dos anos posteriores, [como também Arthur B. Powell, pesquisador em Educação Matemática norte-americano com muitas parcerias de pesquisa em Educação Matemática no Brasil].
Herdando suas propostas e sua determinação e aplicando-as em nossos Centros de Ciências e Matemática e salas de aula, podemos realmente “conectar e seguir com nossas vidas”. Os Centros de Ciências não devem aceitar mais serem considerados como recursos adicionais marginais para o cardápio escolar padrão formalizado e pouco apetitoso, ou reduzidos a mais uma oferta entre as distrações da viagem de campo. Eles são um exemplo metodológico para o ensino agradável de matemática.
Amigos, há um trabalho a ser feito,
há um mundo de criação e alegria a ser vivido junto com todas as crianças,
se ao menos insistirmos em nossos esforços para acompanhar as próprias descobertas dos estudantes,
se insistirmos em uma verdadeira maneira concreta e respeitosa de tratar os estudantes.
Podemos ser justos sobre o sucesso dos Centros de Ciência, seu sucesso formal.
Então, não tenhamos medo!
Maurice Bazin.
Território Indígena do Alto Rio Negro, Brasil, 2004.
Notas:
O texto foi gentilmente cedido ao acervo do Espaço Ciência Viva por Jamie Bell que fez a leitura do texto original na Conferencia ASTC 2004, pois Maurice Bazin não pode comparecer por estar em Projeto Educativo na Floresta Amazônica.
Os negritos, imagens, subtítulos e notas foram inseridos por Paulo Henrique Colonese, editor do site do Espaço Ciência Viva.

