Capa: Os 12 lü (tubos tonais). De Zhu Zaiyu, Yue lü quan shu, c. 1596, vol. 7, seq. 669. Harvard Yenching Library, Rare Book T 6730 2944. (Impresso entre 1736 e 1861.). Nesta representação os 12 tubos tonais estão amarrados, mas eles eram mais comumente mantidos como tubos individuais. Harvard Library Viewer.
- Autor: Moisés Medrado Ribeiro (licenciando em Física, UERJ, bolsista Projeto Prodocência).
- Orientação: Rosana Bulos Santiago (UERJ) e Paulo Henrique Colonese (Espaço Ciência Viva/Museu da Vida Fiocruz).
- Projeto Prodocência: Inovando Metodologias de Ensino de Ciências a partir da colaboração com espaços de ensino formais e não-formais.
Uma escala dodecatônica (12 notas por oitava)
A escala dodecatônica possui 12 notas (as sete notas da escala diatônica acrescida de 5 tons intermediários) dentro de um intervalo musical de oitava.
A escala surgiu na China e influenciou músicos europeus a partir do século XVII, especialmente músicos e matemáticos do século XVIII.
O seu sistema musical divide o intervalo da oitava em 12 partes, todas igualmente espaçadas em uma escala logarítmica, com uma razão igual à 12ª raiz de 2 ( 12 √ 2 ≈ 1,05946).
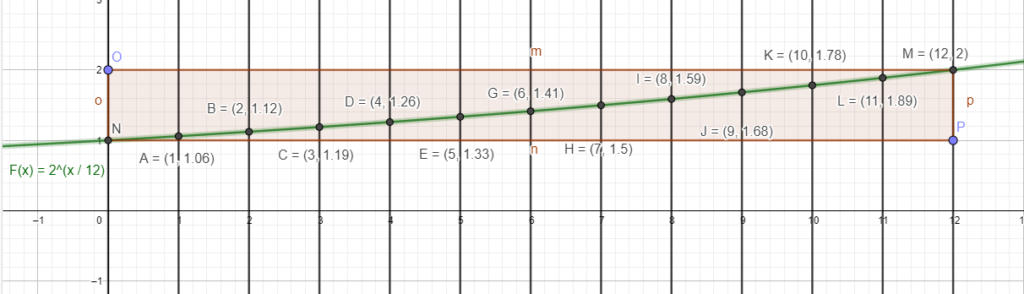
- Observe no gráfico (construído com o software Geogebra Clássico), que o intervalo de oitava de 1 a 2 (eixo Y) é dividido em 12 partes para cada potência natural (de 0 a 12) da raiz duodécima de 2.
- Os pontos indicam (x = potência n, y = valor da raiz elevado a n).
- Obs.: as letras no gráfico não correspondem à notação musical de letras.
O menor intervalo resultante da largura de uma oitava, é chamado de semitom ou meio tom dodecatônico.
O temperamento igual de doze tons é o sistema mais difundido na música hoje.
Tem sido o sistema de afinação predominante da música ocidental, começando com a música clássica , desde o século XVIII, e ela consegue se aproximar em valores absolutos das notas da escala pitagórica.
| ( 12 √ 2)0 | ( 12 √ 2)1 | ( 12 √ 2)2 | ( 12 √ 2)3 | ( 12 √ 2)4 | ( 12 √ 2)5 | ( 12 √ 2)6 |
| 1,000 | 1,059… | 1,122… | 1,189… | 1,260… | 1,334… | 1,414… |
| ( 12 √ 2)7 | ( 12 √ 2)8 | ( 12 √ 2)9 | ( 12 √ 2)10 | ( 12 √ 2)11 | ( 12 √ 2)12 | |
| 1,498… | 1,587… | 1,682… | 1,782… | 1,888… | 2,000 |
ZHU ZAIYU (1536-1611) foi um príncipe da corte chinesa Ming, matemático, físico, coreógrafo e teórico musical chinês. Ele passou trinta anos realizando pesquisas baseadas na ideia de igual temperamento originalmente postulada por seu pai. Ele descreveu sua nova teoria do tons em seu livro Fusion of Music and Calendar, publicado em 1580. Em seguida, publicou um relato detalhado da nova teoria do temperamento igual com uma especificação numérica precisa para os 12-TET (tons igualmente temperados) em seu livro de 5000 páginas Compêndio Completo de Música e Tom ( Yuelü quan shu) em 1584.
Zhu obteve seu resultado matematicamente dividindo o comprimento da corda e do tubo sucessivamente pela duodécima raiz de 2 (12 √ 2 ≈ 1,0594630 e para o comprimento do tubo por 24 √ 2 , tal que após doze divisões (uma oitava) o comprimento foi dividido por um fator de 2:
![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{12}=2}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0e94dc870dfc2af0eb35a7b362eb3776054719)
Da mesma forma, após 84 (7 x 12) divisões (7 oitavas) o comprimento seria dividido por um fator de 128: ![{\displaystyle \left({\sqrt[{12}]{2}}\right)^{84}=2^{7}=128}](https://wikimedia.org/api/rest_v1/media/math/render/svg/efc85da07cabc4f33cc3fc965e9ef6e74361e7c7)
Zhu Zaiyu ilustrou sua teoria do temperamento igual através da construção de um conjunto de 36 tubos de afinação de bambu que variam em 3 oitavas, com instruções sobre o tipo de bambu, cor da tinta e especificações detalhadas sobre seu comprimento e diâmetros interno e externo.
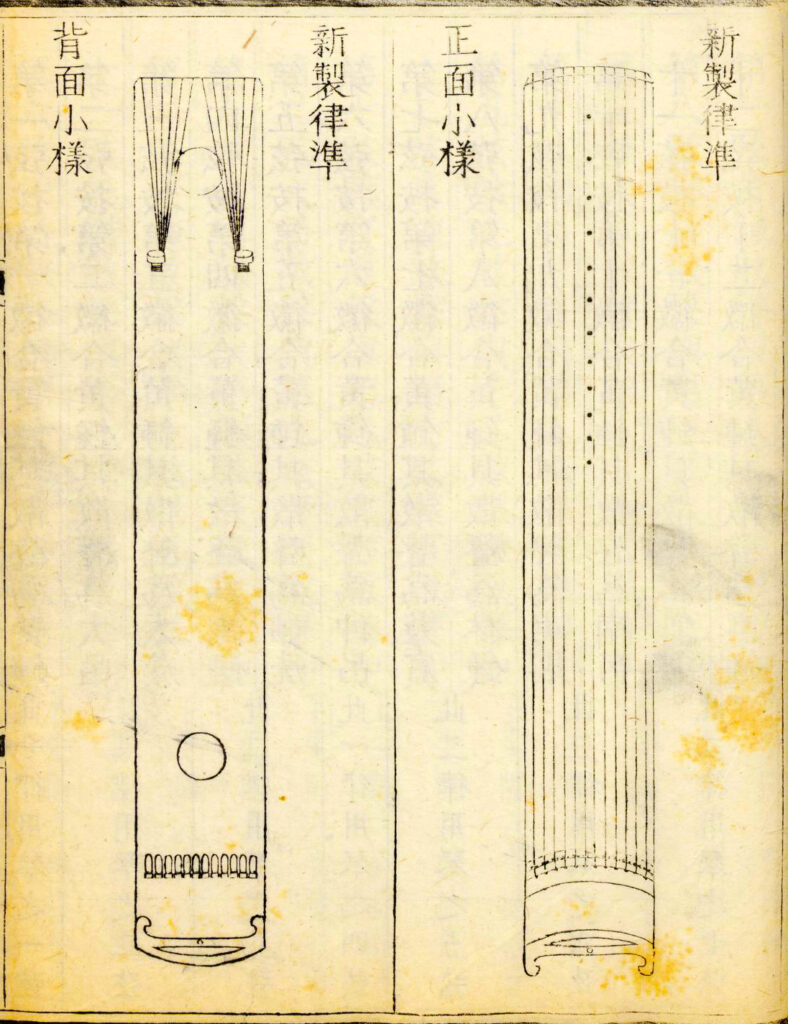
Instrumento musical de 13 notas de Zhu Zaiyu, frente e costas do instrumento. De Zhu Zaiyu. Yue
lü quan shu c. 1596, vol. 1, seq. 34. Harvard Yenching Library, Rare Book T 6730 2944. (Impresso entre 1736 e 1861.) Harward Library Viewer.
Ele também construiu um instrumento de afinação de 12 cordas, com um conjunto de tubos de afinação escondidos dentro de sua cavidade inferior.
Calculando as Frequências
Para encontrar a frequência, Pn , de uma nota no sistema de oitavas de 12 notas, pode-se usar a seguinte definição:
![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(na)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
Nesta fórmula,
- Pn refere-se ao tom, ou frequência (vibrações por segundo) que você está tentando encontrar.
- Pa refere-se à frequência de um tom de referência.
- n e a referem-se a números atribuídos à afinação desejada e à afinação de referência, respectivamente.
A(Lá) 4 (o tom de referência) é a 49ª tecla da extremidade esquerda de um piano (afinado em 440 vibrações por segundo).
E C(Dó) 4 (Dó Central) e F(Fá)# 4 são a 40ª e 46ª tecla, respectivamente, no piano.
Esses números (ordem das teclas) podem ser usados para encontrar a frequência de C(Do’)4 e F(Fá)#4 :
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)
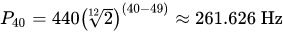
A Escala que influenciou a Europa
O músico Vicenzo Galileu foi um dos primeiros defensores de um sistema dodecatônico de 12 notas, com um sistema ainda baseado em frações (18/17).
Entretanto, a primeira menção de temperamento igual relacionado à raiz décima segunda de dois no Ocidente apareceu no manuscrito de Simon Stevin, Van De Spiegheling der singconst (cerca de 1605), publicado postumamente quase três séculos depois em 1884. No entanto, devido a precisão insuficiente de seu cálculo, muitos dos números de comprimento de corda que ele obteve estavam fora de uma ou duas unidades dos valores corretos.
A escala de 12 notas igualmente temperadas se tornou extremamente importante no século XVIII na música de compositores como Francesco Geminiani, Wilhelm Friedemann Bach, Carl Phillipo Emmanuel Bach e Johann Gottfried Müthel.
Comparando Escalas
Comparando os resultados obtidos pelos processos fracionários e logarítmicos na Escala Justa (fracionária) e Escala Igualmente temperada.
| Intervalo de Dó | Razão para Dó Fundamental Escala Justa | Razão para Dó Fundamental Escala Igualmente Temperada |
|---|---|---|
| Uníssono (Dó-Dó) | 1/1 = 1,0000 | 1,00000 |
| Segunda Menor | 25/24 = 1,0417 | 1,05946 |
| Segunda Maior | 9/8 = 1,1250 | 1,12246 |
| Terça Menor | 6/5 = 1,2000 | 1,18921 |
| Terça Maior | 5/4 = 1,2500 | 1,25992 |
| Quarta | 4/3 = 1,3333 | 1,33483 |
| Quinta Reduzida | 45/32 = 1,4063 | 1,41421 |
| Quinta (Dó-Sol) | 3/2 = 1,5000 | 1,49831 |
| Sexta Menor | 8/5 = 1,6000 | 1,58740 |
| Sexta Maior | 5/3 = 1,6667 | 1,68179 |
| Sétima Menor | 9/5 = 1,8000 | 1,78180 |
| Sétima Maior | 15/8 = 1,8750 | 1,88775 |
| Oitava (Dó-Dó’) | 2,0000 | 2,00000 |
Observe que os processos matemáticos envolvidos para os cálculos são bem diferentes (dois modelos matemáticos diferentes para chegar à harmonia musical). E que os valores são relativamente próximos.
Vamos comparar as frequências obtidas
Para uma escala igualmente temperada com velocidade do som = 345 metros por segundo.
E a Nota Lá4 estabelecida como 440 vibrações por segundo.
Nota Musical da 4a Oitava | Escala Justa (vibrações por segundo) | Escala Igualmente Temperada (vibrações por segundo) | Diferença |
|---|---|---|---|
| C4 | 261.63 | 261.63 | 0 |
| C4# | 272.54 | 277.18 | +4.64 |
| D4 | 294.33 | 293.66 | -0.67 |
| E4b | 313.96 | 311.13 | -2.84 |
| E4 | 327.03 | 329.63 | +2.60 |
| F4 | 348.83 | 349.23 | +0.40 |
| F4# | 367.92 | 369.99 | +2.07 |
| G4 | 392.44 | 392.00 | -0.44 |
| A4b | 418.60 | 415.30 | -3.30 |
| A4 | 436.05 | 440.00 | +3.94 |
| B4b | 470.93 | 466.16 | -4.77 |
| B4 | 490.55 | 493.88 | +3.33 |
| C5 | 523.25 | 523.25 | 0 |
Apesar de as diferenças serem relativamente pequenas, como sua orelha pode ouvir facilmente uma diferença de menos de 1 Hz para notas sustentadas, mesmo diferenças de poucos Hz podem ser bastante significativas!
Os modelos matemáticos para estruturar a harmonia musical não são perfeitos, podem possuir imperfeições ou dissonâncias em algumas de suas possíveis combinações de notas musicais. Isto leva ao contínuo desenvolvimento, aperfeiçoamento e adequação da escala para diferentes instrumentos e diferentes estilos musicais.
Para saber mais
Para conhecer as frequências de várias oitavas com uma escala igualmente temperada, para diferentes escolhas para a frequência de Lá (A), visite a página https://pages.mtu.edu/~suits/notefreqs.html