Capa: Um grupo de músicos renascentistas em The Concert (1623) do pintor holandês Gerard van Honthorst (1592-1656). Wikipédia. Licença de Domínio Público.
- Autor: Moisés Medrado Ribeiro (licenciando em Física, UERJ, bolsista Projeto Prodocência).
- Orientação: Rosana Bulos Santiago (UERJ) e Paulo Henrique Colonese (Espaço Ciência Viva/Museu da Vida Fiocruz).
- Projeto Prodocência: Inovando Metodologias de Ensino de Ciências a partir da colaboração com espaços de ensino formais e não-formais.
O QUE SÃO ESCALAS MUSICAIS?
A orelha humana tem a capacidade de distinguir centenas de sons diferentes em um determinado intervalo musical, definido por duas notas musicais ou sons diferentes que delimitam o intervalo.
Do conjunto de todos esses sons, alguns foram escolhidos e organizados em sequência (do grave ao agudo) para compor um tipo de “alfabeto musical”, os sons das notas musicais, em diferentes culturas.
A relação sonora estética e matemática entre os sons escolhidos – as notas musicais – determina a escala musical criada e adotada.
Escalar o Som
O termo escala musical vem do latim scala, relacionado à ideia de escalar – não uma montanha, indo do ponto mais baixo ao mais alto, mas indo de um som grave (baixo) até o mais agudo (alto). É uma sequência de notas musicais ordenadas da mais grave à mais aguda (ou vice-versa), dentro de um intervalo musical (faixa sonora) escolhido para fins musicais no canto ou em instrumentos musicais.
Diferentes culturas criaram modos diferentes de escolher o conjunto de notas para os diferentes instrumentos musicais que criaram.
Conhecer os padrões de uma escala musical possibilita comunicar ideias musicais entre instrumentos e culturas musicais. Isso permite relacionar e integrar diferentes instrumentos com diferentes intervalos musicais como um piano e uma flauta e criar harmonia entre todos os instrumentos de uma orquestra – o que seria difícil se cada um usasse um padrão musical diferente.
Diversas culturas organizaram diferentes sequências de notas, dando origem a diferentes escalas. E, cada uma, acaba imprimindo uma sensação sonora e estética à música que permitem criar.
Ao ouvirmos uma escala, percebemos que os diferentes intervalos gerados entre uma nota e outra, acabam criando diferentes tipos de sonoridades.
Vamos conhecer alguns tipos mais utilizados de escalas!
Conectando Diferentes Escalas
Um modo de comparar diferentes escalas é considerar um mesmo intervalo musical e descobrir quantas, quais e como as notas se relacionam dentro desse intervalo. Em “Somsacional: Intervalos Musicais”, vimos que os sons graves e agudos se diferenciam pela quantidade de vibrações por segundo (frequência): os graves com valores baixos (vibrações lentas) e os agudos com valores altos (vibrações rápidas).
Para comparar, vamos usar o intervalo musical ocidental mais fundamental, criado desde os pitagóricos, que é o intervalo musical com sons extremos relacionados entre si pelo dobro de frequências: o intervalo chamado de Oitava.
Deste modo, podemos descobrir quantas, quais e como as notas musicais foram determinadas – comparando as notas dentro de uma mesma oitava. Prepare suas orelhas para conhecer algumas escalonamentos de notas musicais:
- Vamos começar conhecendo a Escala Pitagórica Clássica e a Escala Pitagórica Natural e como os pitagóricos (século V a.C.) a construíram usando o princípio de matemática simples: um dos primeiros modelos matemáticos para explicar a harmonia musical.
- Em seguida, convidaremos você a visitar a “Escala de Bach” definida com uma matemática mais sofisticada do início do século XVIII d.C.. Ambas as escalas estão relacionadas musical e matematicamente e foram adotadas em toda a música moderna.
- E finalmente, você poderá conhecer alguns outros tipos de escalas criadas para instrumentos e culturas diferentes no mundo todo.
A Escala Pitagórica
A Música desempenha importante presença na cultura de todas as civilizações. A musicalidade em festas, rituais, comemorações e apresentações a reis e rainhas e o domínio desse saber pode ser tão antiga quanto à pré-história humana.
A Música despertou o interesse de pensadores que buscaram a relação entre a religiosidade que praticavam e a natureza que os cercava. Os filósofos naturais gregos foram primordiais na questão de relacionar a natureza da música a modelos matemáticos e estabeleceram a Música como uma das quatro grandes áreas da Matemática: Aritmética (Número), Geometria (Espaço), Música (Som e Harmonia) e Astronomia (Movimento Celeste).
As relações matemáticas desenvolvidas pelos pitagóricos seriam uma expressão da própria divindade,
descrita com um simbolismo particular: a linguagem matemática, cuja essência espiritual eram os Números.

Pitágoras de Samos (570 a.C – 495 a.C), observou que duas cordas semelhantes na mesma tensão e estando diferentes apenas em comprimento, quando tocadas juntas criam um efeito que é agradável à audição se os comprimentos das cordas tiverem como quociente (razão) dois números naturais pequenos, tais como
1/1, 1/2, 2/3, 3/4, 4/5, 5/6 e 2/1.
Construindo uma Escala Pitagórica
Se a razão dos comprimentos for de 1 para 2 ( 1/2 ou 0,5), então eles correspondem ao intervalo de uma oitava musical, com os comprimentos maiores produzindo sons graves e os menores, sons agudos.
Usando as frações simples 1/2 , 2/3 e 3/4, os pitagóricos criaram um procedimento para encontrar os comprimentos das notas musicais consideradas “em harmonia” no intervalo de oitava dos comprimentos L e L/2.
| L | (8/9)L | (64/81)L | (3/4)L | (2/3)L | (16/27)L | (128/243)L | (1/2)L | (4/9)L | (32/81)L |
| 1 | 8/9 0,888… | 64/81 0,790… | 3/4 0,75 | 2/3 0,666… | 16/27 0,592… | 128/243 0,526… | 1/2 0,5 | 4/9 0,444… | 32/81 0,395… |
| 1 nota mais grave | 2 | 3 | 4 | 5 | 6 | 7 | 8 nota mais aguda | Fora do intervalo. | Fora do intervalo. |
- Partimos de um comprimento L.
- Aplicamos (2/3, cerca de 0,67), e obtemos uma nota no intervalo.
- Se aplicarmos (2/3) novamente, teremos (4/9)L. Uma nota fora do intervalo.
- Multiplicando por 2, obtemos (8/9)L, novamente dentro do intervalo.
- Aplicando (2/3) novamente, obtemos (16/27)L, também dentro do intervalo.
- Aplicando (2/3), obtemos (32/81)L, fora do intervalo.
- Multiplicando por 2, obtemos (64/81)L, mais uma nota no intervalo.
- Aplicando (2/3), obtemos (128/243)L, dentro do intervalo.
- Como os denominadores e numeradores estão chegando a valores elevados, podemos continuar com uma fração simples, como (3/4)L, dentro do intervalo.
E assim, concluímos as notas escolhidas matematicamente pelos pitagóricos para criar um conjunto de notas consideradas “harmônicas” entre si.
Procedimento a partir do comprimento de cordas/tubos
| Determine um comprimento musical inicial. | Divida o comprimento por 3, então multiplique por 2. | O novo comprimento está dentro dos limites da oitava? | Não? (n < L/2) Multiplique o comprimento por 2. 2n e recomece. |
| L | n = (2/3)L | L/2 < n < L | Sim? (L/2 < n < L) Você obteve uma nova nota musical. Comece novamente com este valor! |
Veja no vídeo abaixo, uma visualização da construção de uma oitava de cordas, a partir de frações simples do comprimento inicial de uma corda.
Procedimento por meio de frequências (vibrações por segundo)
Podemos, atualmente, usar os produtos com numeradores e denominadores “simples” (naturais): 2; 3/2 e 4/3 para encontrar as frequências dentro do intervalo de frequências F e 2F. Vejamos um procedimento completo para as frequências.
| Escolha / determine uma frequência inicial | Multiplique a frequência por 3, e divida por 2 | A nova frequência está dentro dos limites da oitava? | Não! (n > 2f) Divida a frequência por 2 n / 2 |
| f | n = (3/2)f | f < n < 2f | Sim! (n<2f) Você obteve uma nova nota musical. Comece novamente com este valor! |
Digamos que você queira construir uma nota musical na escala, aos moldes gregos. Para isso, precisaríamos pegar uma corda que produza um som f, considerando esta corda como o início de uma oitava e 2f, o fim da oitava.
| 1F | (9/8)F | (81/64)F | (4/3)F | (3/2)F | (27/16)F | (243/128)F | 2F | (9/4)F | (81/32)F |
| 1/1 1,0 | 9/8 1,125 | 81/64 1,265… | 4/3 1,333… | 3/2 1,5 | 27/16 1,6875 | 243/128 1,898… | 2/1 2,0 | 9/4 2,25 | 81/32 2,53125 |
| fora do intervalo | fora do intervalo |
ordenadas da mais grave para a mais aguda.
- Iniciamos com uma frequência f qualquer.
- Aplicando três meios (3/2) à frequência, obtemos uma nota de tom mais alto (3/2)F, dentro do intervalo 1:2.
- Se aplicarmos 3/2 a (3/2)F, teremos (9/4)F, imediatamente fora do intervalo.
- Se dividirmos essa nota por dois, teremos (9/8)F, voltando à oitava inicial.
- Se aplicarmos 3/2 a (9/8)F, obtemos (27/16)F, mais uma nota dentro do intervalo.
- Se aplicarmos 3/2 a (27/16)F, obtemos (81/32)F, imediatamente fora do intervalo.
- Se dividirmos essa nota por dois, obtemos (81/64)F, dentro do intervalo.
- Se aplicarmos 3/2 a (81/64)F, obtemos (243/128)F, dentro do intervalo.
Aqui, as frações deixam de ter valores “simples” para numeradores e denominadores, e podemos completar a escala com a fração (4/3)F, completando 8 notas de F a 2F.
| F | (9/8)F | (81/64)F | (4/3)F | (3/2)F | (27/16)F | (243/128)F | 2F | (9/4)F | (81/32)F |
| 1/1 1,0 | 9/8 1,125 | 81/64 1,265… | 4/3 1,333… | 3/2 1,5 | 27/16 1,687… | 243/128 1,898… | 2/1 2,0 | 9/4 2,25 | 81/32 2,53125 |
| 1a | Segunda | Terça | Quarta | Quinta | Sexta | Sétima | Oitava | fora do intervalo | fora do intervalo |
| Dó | Ré | Mi | Fá | Sol | Lá | Si | Dó |
ordenadas da mais grave para a mais aguda.
Se escolhermos como primeira nota, a nota dó, criaremos o intervalo da Oitava de Dó, de acordo com a nomenclatura atual. Observe que o método não fornece as notas em ordem, precisamos ordená-las ao final da mais grave à mais aguda para chegar à ordenação: dó-ré-mi-fá-sol-lá-si-dó.
O conceito desta escala é portanto simples: determinar as “quintas notas” (3/2) e transportá-las para dentro da oitava inicial, seguindo o algoritmo pitagórico, adaptado para frequências.
Pitágoras ficou tão impressionado por esta descoberta que a tornou a base de uma escola – chamada Escola Pitagórica – que mantinham crenças místicas, atribuindo um grande poder aos números.
O princípio de tudo é o Número. Escola Pitagórica.
A oitava atualmente é usada na Música Clássica moderna, no Jazz, nas músicas “nordestinas” (comum no baião, frevos e em diversos outros estilos musicais desta região).
Escala Pitagórica e o Violão…
Veja no vídeo abaixo, uma visualização da construção de uma oitava de cordas, assim como vimos no último vídeo! Porém, ao final, o apresentador termina falando da correção necessária para criar a escala temperada/cromática.
Se você se interessou pelo “problema da última nota”, acesse o link do post que fala sobre a Escala Cromática (Bach):
Seguindo, vamos esmiuçar um pouco o problema entre as razões das notas na escala pitagórica…
Nem todo Modelo é Perfeito
Se calcularmos os intervalos – definido pelo quociente (razão) entre todas as alturas (frequências) da escala pitagórica, obtemos uma certa regularidade com apenas dois valores:
- 9/8 = 1,125
- 256/243 = 1,05349794239
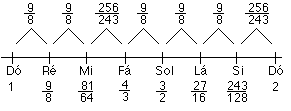
Chamados respectivamente de tom pitagórico diatónico e semitom pitagórico diatónico. Obtém-se assim uma escala com 7 notas diferentes separadas por tons 5 tons e 2 semitons, um tipo de Escala Heptatônica (hepta = sete, tônica = tons (7 notas em cada oitava) que fundamentou a música europeia, constituída por tons e semi-tons na sequência: T – T – ST – T – T – T – ST (maior). Isto padronizou a Escala Pitagórica Heptatônica Clássica.
Os estudos de razões “harmônicas” e proporções simples foram a essência da música durante a época dos pitagóricos.
A partir da Idade Média, com o surgimento de músicas mais complexas, observou-se que, embora as razões fossem “perfeitas”, ocorriam problemas quando alguns conjuntos de notas, diferentes tonalidades ou escalas com mais notas eram utilizadas.
Surgiu, então, a necessidade de aprimorar o modelo matemático, e criar um sistema de afinação alternativo e também outras definições de escala musicais – que foram sendo criadas com mais ferramentas matemáticas criadas com o avanço da matemática e pelo aprimoramento de instrumentos musicais.
Conheça algumas outras escalas nos links abaixo:
Escala Igualmente Temperada: A Escala que veio da China.

