Tangram Chinês (Qí qiao ban)

Nome: o seu nome original chinês é qí qiao ban (qí = sete, qiao = hábil, engenhosa, significando as sete peças engenhosas). Ao ser levado para a Europa, foi renomeado com termos latinizados como Tangram, termo composto por Tang, representando uma grande dinastia chinesa e gram, de diagrama, significando literalmente Diagramas Chineses.

Alguns comerciantes atualmente adotam o nome fantasia de Tangran com “n”. Como atualmente existe uma variedade de jogos de composição adotando o nome Tangram ou Tangran, recomendamos o uso de Tangram Chinês, para diferenciar o jogo original.

Áreas da Matemática: Geometria Plana.

Breve Histórico

É um jogo cultural de origem chinesa, um quebra-cabeça geométrico de decomposição, composição e transformação de formas.

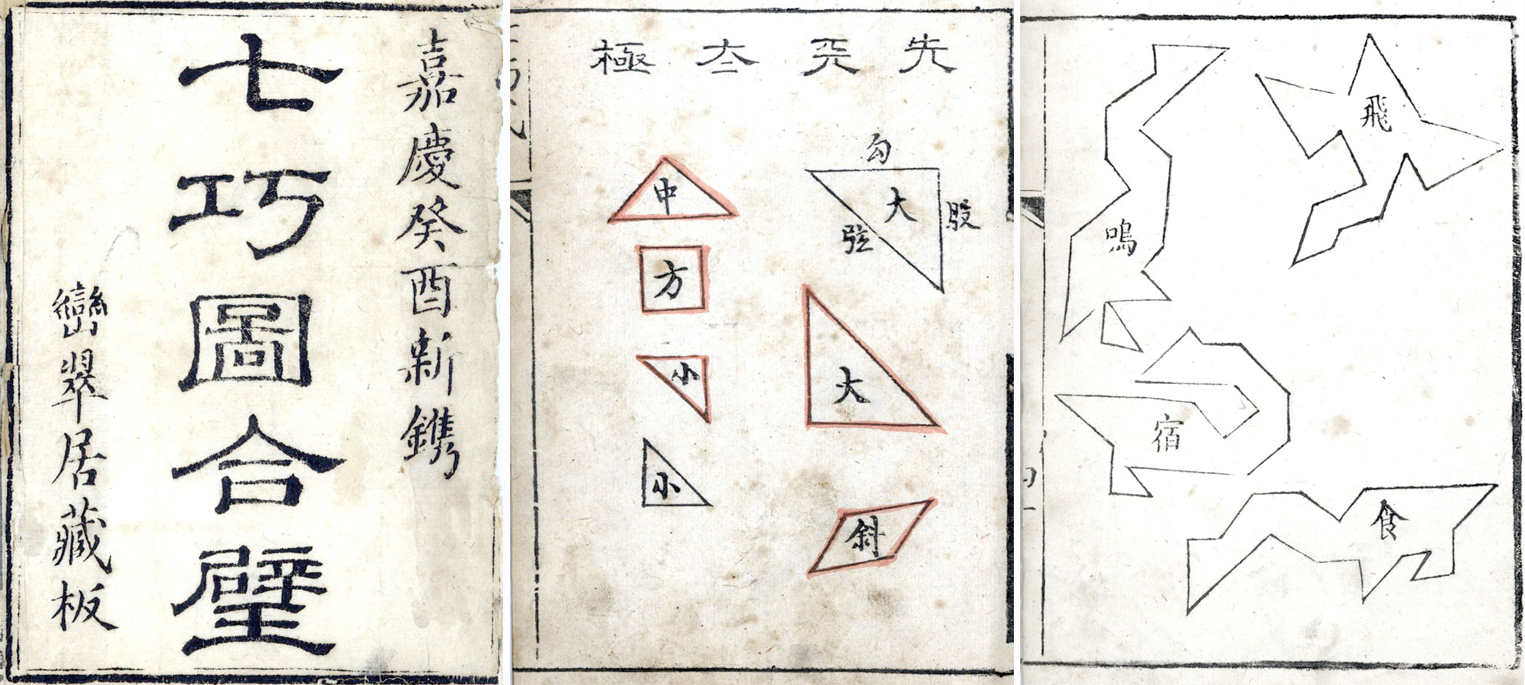
É formado a partir de um quadrado que foi decomposto em sete peças planas (1 quadrado, 5 triângulos retângulos (2 grandes, 1 médio e 2 pequenos) e 1 paralelogramo não retangular) utilizadas para a criação de inúmeras figuras do tipo silhueta.

Um jogo semelhante, o Loculus de Arquimedes, é outra decomposição de um quadrado, datado do século III a.C. [in Slocum and Hotermans]. Talvez o jogo mais antigo registrado de composição e decomposição da história.

O jogo japonês Sei Shonagon Chie-no-ita introduzido em 1700 é bastante similar e pode ter influenciado o jogo chinês. Temos menção ao jogo e publicações no século XVIII, mas a primeira obra conhecida é de 1813 ( Compilação de Diagramas Tangram de Bi Wu Jushi e Sang Xia Ke) e já continha cerca de 200 figuras para serem montadas pelas sete peças. De lá para cá, inúmeros educadores e fãs do jogo tem publicado livros com dezenas ou milhares de figuras produzidas pelas sete peças.

Classificação quanto à Função Educativa

• (X ) Ilustrativo ou descritivo.
• (X)  Analítico ou de observação.
• (X) Experimental.
• (X) Demonstrativo.

O Tangram Chinês pode ser usado em qualquer uma das modalidades, dependendo dos objetivos educacionais.

Classificação quanto à Origem

• ( X ) Jogo de origem cultural (quebra-cabeças geométrico de composição).
• (   ) Jogo de origem escolar, curricular.

Apesar de ser atualmente muito utilizado em projetos educacionais no âmbito escolar, a origem do jogo é cultural, tendo sido criado fora do âmbito curricular.

Classificação quanto à estrutura do jogo

• (X) Jogo de livre criação.
• (X) Jogo com regras.
• (X) Jogo com desafios estruturados.

O Tangram Chinês permite a criação de atividades de todos os três tipos, desde a criação livre de figuras até desafios estruturados em diferentes níveis de dificuldade.

Descrição / Construção do material

• Quebra-cabeças formado por 7 peças: triângulos retângulos isósceles (2 grandes, 1 médio e 2 pequenos); 1 quadrado e 1 paralelogramo inclinado. Pode ser construído com diferentes materiais, mas para um uso permanente recomendamos a construção em MDF ou algum material mais resistente.
• É um jogo de silhueta que desafia o jogador a imaginar as possíveis decomposições da figura e, ao mesmo tempo, ao final, a visualizar a figura completa. Deste modo, sugerimos usar as peças com a mesma cor. De modo a deixar a decomposição a ser imaginada e construída pela mente do jogador. Uma sugestão para investigar as propriedades de simetria das 7 peças, é usar a mesma cor na frente, e outra cor nos fundos das peças.
• O jogo pode ter uma base de uma cor com um buraco quadrado para formação do quadrado e guarda das peças.
• Dimensões quadrado completo: 18 cm x 18 cm.
• Dimensões da base: 24 cm x 24 cm.
• As fichas com diferentes diagramas podem ser impressas em A4 na mesma escala das peças (para iniciantes) e em escalas diferentes (para experientes).

Cadernos e Material Didático  ESPAÇO CIÊNCIA VIVA

• Caderno para professores: “Explorações Geométricas. Estéticas e Literárias com o Tangram Chinês”, Paulo Henrique Colonese, Universidade Severino Sombra, Espaço Ciência Viva, 2014.
• Fichas de desafios geométricos. Paulo Henrique Colonese. Universidade Severino Sombra, Espaço Ciência Viva, 2014.

Alguns Fabricantes

• PERFORMA MATERIAIS PEDAGÓGICOS, Sólidos Geométricos. 1 jogo de dimensões 18 cm x 18 cm, com base em MVA.
• SELLER. Tangram de borracha (EVA). Kit com 1 jogo de dimensões: 5 cm x 21,5 cm x 11 cm.
• ABC BRINQUEDOS EDUCATIVOS. Tangram emborrachado. Kit com 1 jogo de dimensões (retângulo): 13 x 24 x 0,8 cm.
• ABC BRINQUEDOS EDUCATIVOS. Tangram em madeira MDF reflorestada. Dimensões: 17 x 17 x 6,5 cm. Kit com 10 jogos.
• XALINGO BRINQUEDOS. Tangran! (nome fantasia) em madeira. Kit com 4 jogos. Caixa de dimensões: 24 cm x 5 cm x 18 cm.
• NEW ART DO BRASIL. Tangram em madeira. (tamanho normal) e (tamanho gigante).

Tangram Chinês em Museus

Conexões Curriculares Educação Infantil: RCNEI, Educação Infantil, Matemática (4-6 anos)

Conexões Curriculares Educação Infantil: RCNEI, Educação Infantil, Matemática (4-6 anos)

Objetivos Gerais

• O1. Reconhecer e valorizar os números, as operações numéricas, as contagens orais e as noções espaciais como ferramentas necessárias no seu cotidiano;
• O2. Comunicar ideias matemáticas, hipóteses, processos utilizados e resultados encontrados em situações-problema relativas a quantidades, espaço físico e medida, utilizando a linguagem oral e a linguagem matemática;
• O3. Ter confiança em suas próprias estratégias e na sua capacidade para lidar com situações matemáticas novas, utilizando seus conhecimentos prévios.

Números

• N1. Utilização da contagem oral nas brincadeiras e em situações nas quais as crianças reconheçam sua necessidade.
• N3. Comunicação de quantidades, utilizando a linguagem oral, a notação numérica e/ou registros não convencionais.

Grandezas e Medidas

• M1. Exploração de diferentes procedimentos para comparar grandezas.
• M2. Introdução às noções de medida de comprimento, peso, volume e tempo, pela utilização de unidades convencionais e não convencionais.

Espaço e Forma

• E1. Explicitação e/ou representação da posição de pessoas e objetos, utilizando vocabulário pertinente nos jogos, nas brincadeiras e nas diversas situações nas quais as crianças considerarem necessário essa ação.
• E2. Exploração e identificação de propriedades geométricas de objetos e figuras, como formas, tipos de contornos, bidimensionalidade, tridimensionalidade, faces planas, lados retos etc.
• E3. Representações bidimensionais e tridimensionais de objetos.

Orientações didáticas para Educação Infantil (4 a 6 anos)

• Quantificar a quantidade de peças utilizadas nas figuras (1 a 7 peças)
• Ordenar as peças por área: maior / menor / iguais.
• Ordenar as figuras pela quantidade de peças utilizadas (1 a 7)
• Comparar as peças: triângulos isósceles retângulos (2 lados iguais, uma “quina” reta); quadrado (quinas retas) e paralelogramos.
• O quebra-cabeça deve ser explorado principalmente para a criação livre e o registro por desenho de figuras com as peças do jogo.
• A quantidade de peças pode ser de escolha livre das crianças.
• Criar histórias com as figuras produzidas ou com as fichas desafio.
• Criar apelidos para as figuras.
• Criar obras de arte geométricas com as peças.
• Criar desenhos com os contornos das peças.
• Utilizar desafios com quantidade reduzida de peças (1 a 4 peças).

Conexões com Objetivos e Conteúdos Curriculares: PCN, Ensino Fundamental I, Ciclo 1

Objetivos de Matemática

• O7. Perceber semelhanças e diferenças entre objetos no espaço, identificando formas tridimensionais ou bidimensionais, em situações que envolvam descrições orais, construções e representações.
• O8. Reconhecer grandezas mensuráveis, como comprimento, massa, capacidade e elaborar estratégias pessoais de medida.
• O10. Utilizar instrumentos de medida, usuais ou não, estimar resultados e expressá-los por meio de representações não necessariamente convencionais.

Números e Sistema de Numeração

• N1. Reconhecimento de números no contexto diário.
• N2. Utilização de diferentes estratégias para quantificar elementos de uma coleção: contagem, pareamento, estimativa e correspondência de agrupamentos.
• N3. Utilização de diferentes estratégias para identificar números em situações que envolvem contagens e medidas.
• N4. Comparação e ordenação de coleções pela quantidade de elementos e ordenação de grandezas pelo aspecto da medida.

Espaço e Forma

• E1. Localização de pessoas ou objetos no espaço, com base em diferentes pontos de referência e algumas indicações de posição.
• E2. Movimentação de pessoas ou objetos no espaço, com base em diferentes pontos de referência e algumas indicações de direção e sentido.
• E3. Descrição da localização e movimentação de pessoas ou objetos no espaço, usando sua própria terminologia.
• E4. Dimensionamento de espaços, percebendo relações de tamanho e forma.
• E9. Construção e representação de formas geométricas.

  Grandezas e Medidas

• M1. Comparação de grandezas de mesma natureza, por meio de estratégias pessoais e uso de instrumentos de medida conhecidos — fita métrica, balança, recipientes de um litro, etc.

  Atitudes e Valores

•  A1. Desenvolvimento de atitudes favoráveis para a aprendizagem de Matemática.
• A2. Confiança na própria capacidade para elaborar estratégias pessoais diante de situações-problema.
• A3. Valorização da troca de experiências com seus pares como forma de aprendizagem.
• A6. Valorização da utilidade dos elementos de referência para localizar-se e identificar a localização de objetos no espaço.
• A7. Sensibilidade pela observação das formas geométricas na natureza, nas artes, nas edificações.
• A10. Apreciação da organização na elaboração e apresentação dos trabalhos.

Conexões com Objetivos e Conteúdos Curriculares: PCN, Ensino Fundamental I, Ciclo 2

Objetivos de Matemática

• O2. Construir o significado do número racional e de suas representações (fracionária e decimal), a partir de seus diferentes usos no contexto social.
• O7. Estabelecer pontos de referência para interpretar e representar a localização e movimentação de pessoas ou objetos, utilizando terminologia adequada para descrever posições.
• O8. Identificar características das figuras geométricas, percebendo semelhanças e diferenças entre elas, por meio de composição e decomposição, simetrias, ampliações e reduções.
• O11. Identificar características de acontecimentos previsíveis ou aleatórios a partir de situações-problema, utilizando recursos estatísticos e probabilísticos.
• O12. Construir o significado das medidas, a partir de situações-problema que expressem seu uso no contexto social e em outras áreas do conhecimento e possibilitem a comparação de grandezas de mesma natureza.
• O13. Utilizar procedimentos e instrumentos de medida usuais ou não, selecionando o mais adequado em função da situação-problema e do grau de precisão do resultado.

Números e Sistema de Numeração

• N1. Reconhecimento de números naturais e racionais no contexto diário.
• N10. Exploração dos diferentes significados das frações em situações-problema: parte/todo, quociente e razão.

Espaço e Forma

• E1. Descrição, interpretação e representação da posição de uma pessoa ou objeto no espaço, de diferentes pontos de vista.
• E2. Utilização de malhas ou redes para representar, no plano, a posição de uma pessoa ou objeto.
• E11. Identificação de semelhanças e diferenças entre polígonos, usando critérios como número de lados, número de ângulos, eixos de simetria, etc.
• E13. Composição e decomposição de figuras planas e identificação de que qualquer polígono pode ser composto a partir de figuras triangulares.
• E14. Ampliação e redução de figuras planas pelo uso de malhas.
• E15. Percepção de elementos geométricos nas formas da natureza e nas criações artísticas.
• E16. Representação de figuras geométricas.

Grandezas e Medidas

• M1. Comparação de grandezas de mesma natureza, com escolha de uma unidade de medida da mesma espécie do atributo a ser mensurado.
• M10. Cálculo de perímetro e de área de figuras desenhadas em malhas quadriculadas e comparação de perímetros e áreas de duas figuras sem uso de fórmulas.

Atitudes e Valores

• A2. Perseverança, esforço e disciplina na busca de resultados.
• A4. Respeito pelo pensamento do outro, valorização do trabalho cooperativo e do intercâmbio de ideias, como fonte de aprendizagem.
• A9. Valorização da utilidade dos sistemas de referência para localização no espaço.
• A10. Sensibilidade para observar simetrias e outras características das formas geométricas, na natureza, nas artes, nas edificações.
• A11. Curiosidade em conhecer a evolução histórica das medidas, unidades de medida e instrumentos utilizados por diferentes grupos culturais e reconhecimento da importância do uso adequado dos instrumentos e unidades de medida convencionais.

Orientações didáticas para Ensino Fundamental I (Ciclos 1 e 2)

• Quantificar: peças, triângulos, quadrados e paralelogramos.
• Observar diferenças e congruências nos comprimentos dos lados e nas medidas dos ângulos por sobreposição das peças.
• Explorar experimentalmente as relações fracionárias entre as áreas de figuras planas.
• Ordenar as peças: maior / menor / iguais.
• Comparar por sobreposição a área das peças e os lados e perímetros da figuras,
• Comparar as peças: triângulos isósceles retângulos (2 lados iguais, uma “quina” reta); quadrado (quinas retas) e paralelogramos.
• Produzir textos escritos e ilustrados com as figuras do Tangram.
• Observar as soluções dos colegas aos desafios propostos.
• Criar e propor desafios aos colegas.
• Construir histórias individuais e coletivas com as figuras criadas com o Tangram.
• Desafiar os estudantes a criar figuras livremente ou poligonais com maior dificuldade (de 2 a 5 peças).
• Explorar os desafios de figuras poligonais em escala crescente de dificuldade (aumentando a quantidade de peças na figura).
• Registrar as soluções encontradas por desenho livre e depois em papel quadriculado (desenho em escala) com a finalidade de encontrar várias soluções possíveis.
• Comparar as diferenças e semelhanças entre as várias soluções de uma mesma figura (quantidade de peças, disposição (vizinhança) das peças na figura).
• Comparar visualmente e por sobreposição as áreas das peças, envolvendo as relações de metade, um quarto e um oitavo ou dobro e quádruplo, de acordo com a peça unidade escolhida.

Conexões com Objetivos e Conteúdos Curriculares: PCN, Ensino Fundamental II (Ciclo 3 )

Objetivos de Matemática

Pensamento geométrico

• O9. Resolver situações-problema de localização e deslocamento de pontos no espaço, reconhecendo nas noções de direção e sentido, de ângulo, de paralelismo e de perpendicularismo elementos fundamentais para a constituição de sistemas de coordenadas cartesianas;
• O10. Estabelecer relações entre figuras espaciais e suas representações planas, envolvendo a observação das figuras sob diferentes pontos de vista, construindo e interpretando suas representações;
• O11. Resolver situações-problema que envolvam figuras geométricas planas, utilizando procedimentos de decomposição e composição, transformação, ampliação e redução.

 Competência métrica

• O12. Ampliar e construir noções de medida, pelo estudo de diferentes grandezas, a partir de sua utilização no contexto social e da análise de alguns dos problemas históricos que motivaram sua construção;
• O13. Resolver problemas que envolvam diferentes grandezas, selecionando unidades de medida e instrumentos adequados à precisão requerida.

Números e Sistema de Numeração

• N4. Reconhecimento de números racionais em diferentes contextos cotidianos e históricos e exploração de situações-problema em que indicam relação parte/todo, quociente, razão ou funcionam como operador.
• N7. Compreensão da raiz quadrada e cúbica de um número, a partir de problemas como a determinação do lado de um quadrado de área conhecida ou da aresta de um cubo de volume dado.

Medidas e Grandezas

• M1. Reconhecimento de grandezas como comprimento, massa, capacidade, superfície, volume, ângulo, tempo, temperatura, velocidade e identificação de unidades adequadas (padronizadas ou não) para medi-las, fazendo uso de terminologia própria.
• M4. Utilização de instrumentos de medida, como régua, escalímetro, transferidor, esquadro, trena, relógios, cronômetros, balanças para fazer medições, selecionando os instrumentos e unidades de medida adequadas à precisão que se requerem, em função da situação-problema.
• M5. Compreensão da noção de medida de superfície e de equivalência de figuras planas por meio da composição e decomposição de figuras.
• M6. Cálculo da área de figuras planas pela decomposição e/ou composição em figuras de áreas conhecidas, ou por meio de estimativas.

Espaço e Forma

• E2. Distinção, em contextos variados, de figuras bidimensionais e tridimensionais, descrevendo algumas de suas características, estabelecendo relações entre elas e utilizando nomenclatura própria.
• E3. Classificação de figuras tridimensionais e bidimensionais, segundo critérios diversos, como: corpos redondos e poliedros; poliedros regulares e não regulares; prismas, pirâmides e outros poliedros; círculos, polígonos e outras figuras; número de lados dos polígonos; eixos de simetria de um polígono; paralelismo de lados, medidas de ângulos e de lados.
• E4. Composição e decomposição de figuras planas.
• E6. Transformação de uma figura no plano por meio de reflexões, translações e rotações e identificação de medidas que permanecem invariantes nessas transformações (medidas dos lados, dos ângulos, da superfície).
• E7. Ampliação e redução de figuras planas segundo uma razão e identificação dos elementos que não se alteram (medidas de ângulos) e dos que se modificam (medidas dos lados, do perímetro e da área).

Atitudes e Valores

• A1. Desenvolvimento da capacidade de investigação e da perseverança na busca de resultados, valorizando o uso de estratégias de verificação e controle de resultados.
• A2. Predisposição para alterar a estratégia prevista para resolver uma situação-problema quando o resultado não for satisfatório.
• A3. Reconhecimento que pode haver diversas formas de resolução para uma mesma situação-problema e conhecê-las.
• A4. Valorização e uso da linguagem matemática para expressar-se com clareza, precisão e concisão.
• A5. Valorização do trabalho coletivo, colaborando na interpretação de situações-problema, na elaboração de estratégias de resolução e na sua validação.

Conexões com Objetivos e Conteúdos Curriculares: PCN, Ensino Fundamental II (Ciclo 4)

Pensamento geométrico

• O7. Interpretar e representar a localização e o deslocamento de uma figura no plano cartesiano; produzir e analisar transformações e ampliações/reduções de figuras geométricas planas, identificando seus elementos variantes e invariantes, desenvolvendo o conceito de congruência e semelhança;
• O8. Ampliar e aprofundar noções geométricas como incidência, paralelismo, perpendicularismo e ângulo para estabelecer relações, inclusive as métricas, em figuras bidimensionais e tridimensionais.

Competência métrica:

• O9. Ampliar e construir noções de medida, pelo estudo de diferentes grandezas, utilizando dígitos significativos para representar as medidas, efetuar cálculos e aproximar resultados de acordo com o grau de precisão desejável;
• O10. Obter e utilizar fórmulas para cálculo da área de superfícies planas e para cálculo de volumes de sólidos geométricos (prismas retos e composições desses prismas).

Números e Sistema de Numeração

• N1. Constatação que existem situações-problema, em particular algumas vinculadas à Geometria e medidas, cujas soluções não são dadas por números racionais (caso de pi, da raiz quadrada de 2, de 3 etc.).

Medidas e Grandezas

• M2. Cálculo da área de superfícies planas por meio da composição e decomposição de figuras e por aproximações.
• M3. Construção de procedimentos para o cálculo de áreas e perímetros de superfícies planas (limitadas por segmentos de reta e/ou arcos de circunferência).
• M6. Análise das variações do perímetro e da área de um quadrado em relação à variação da medida do lado e construção dos gráficos cartesianos para representar essas interdependências.

Espaço e Forma

• E9. Verificação da validade da soma dos ângulos internos de um polígono convexo para os polígonos não convexos.
• E14. Desenvolvimento da noção de semelhança de figuras planas a partir de ampliações ou reduções, identificando as medidas que não se alteram (ângulos) e as que se modificam (dos lados, da superfície e perímetro).

Atitudes e Valores

• A1. Desenvolvimento da capacidade de investigação e da perseverança na busca de resultados, valorizando o uso de estratégias de verificação e controle de resultados.
• A2. Predisposição para alterar a estratégia prevista para resolver uma situação-problema quando o resultado não for satisfatório.
• A3. Reconhecimento que pode haver diversas formas de resolução para uma mesma situação-problema e conhecê-las.

Orientações Didáticas para Ensino Fundamental II (Ciclo 3 e 4)

• Quantificar: peças, triângulos, quadrados e paralelogramos.
• Observar diferenças e congruências nos comprimentos dos lados e nas medidas dos ângulos por sobreposição das peças.
• Quantificar as relações fracionárias entre as áreas de figuras planas.
• Comparar por sobreposição a área das peças.
• Adotar a área de uma peça como unidade de área,
• Medir a área das peças de acordo com a peça unidade adotada.
• Comparar por sobreposição os lados e perímetros das figuras,
• Comparar as peças: triângulos isósceles retângulos (2 lados iguais, uma “quina” reta); quadrado (quinas retas) e paralelogramos.
• Produzir textos escritos e ilustrados (histórias) com as figuras do Tangram, em escala correta.
• Observar as soluções dos colegas aos desafios propostos.
• Criar e propor desafios aos colegas.
• Buscar coletivamente todas as soluções dos desafios poligonais.

Conexões Curriculares: Competências e Habilidades Matemáticas, PCN(+)Ensino Médio

  Representação e Comunicação

• RC8. Expressar-se com clareza, utilizando a linguagem matemática, elaborando textos, desenhos, gráficos, tabelas, equações, expressões e escritas numéricas – para comunicar-se via internet, jornais ou outros meios, enviando ou solicitando informações, apresentando ideias, solucionando problemas.
• RC10. Expressar-se da forma oral para comunicar ideias, aprendizagens e dificuldades de compreensão; por exemplo, explicando a solução dada a um problema, expondo dúvidas sobre um conteúdo ou procedimento, propondo e debatendo questões de interesse.

Discussão e Argumentação

• RC11. Compreender e emitir juízos próprios sobre informações relativas à ciência e tecnologia, de forma analítica e crítica, posicionando-se com argumentação clara e consistente sempre que necessário, identificar corretamente o âmbito da questão e buscar fontes onde possa obter novas informações e conhecimentos. Por exemplo, ser capaz de analisar e julgar cálculos efetuados sobre dados econômicos ou sociais, propagandas de vendas a prazo, probabilidades de receber determinado prêmio em sorteios ou loterias, ou ainda apresentadas em um dado problema ou diferentes sínteses e conclusões extraídas a partir de um mesmo texto ou conjunto de informações.

Investigação e Compreensão: Medidas, Grandezas e Escalas

• IC9. Identificar e fazer uso de diferentes formas e instrumentos apropriados para efetuar medidas ou cálculos; por exemplo, discriminar o melhor instrumento para medir, comparar ou calcular comprimentos e distâncias, ângulos, volumes ocupados por líquidos, em dada situação específica. Usar adequadamente réguas, esquadros, transferidores, compassos, calculadoras e outros instrumentos ou aparelhos.
• IC12. Compreender a necessidade e fazer uso apropriado de escalas; por exemplo, na construção de gráficos ou em representações de plantas e mapas.

  Contextualização sociocultural: Ciência e Tecnologia na cultura contemporânea

• CSC4. Compreender a Matemática como parte integrante da cultura contemporânea, sendo capaz de identificar sua presença nas manifestações artísticas ou literárias, teatrais ou musicais, nas construções arquitetônicas ou na publicidade.

Conexões Curriculares: Temas e Conteúdos, PCN(+)Ensino Médio

Geometria plana

• GP4. Utilizar as propriedades geométricas relativas aos conceitos de congruência e semelhança de figuras.
• GP5. Fazer uso de escalas em representações planas.

Métrica

• M1. Identificar e fazer uso de diferentes formas para realizar medidas e cálculos.
• M2. Utilizar propriedades geométricas para medir, quantificar e fazer estimativas de comprimentos, áreas e volumes em situações reais relativas, por exemplo, de recipientes, refrigeradores, veículos de carga, móveis, cômodos, espaços públicos.

Orientações Didáticas para Ensino Médio

• Encontrar todas as soluções para os 13 polígonos convexos de 7 peças.
• Provar que existem apenas 13 polígonos convexos de 7 peças.

Conexões Literárias e Midiáticas

• BIESEMEYER, I. B. Os animais do mundinho. Editora Difusão Cultural do Livro, 2007, ISBN-13:9788536803029, ISBN-10: 8536803029. Livro com animais ilustrados em Tangram.
• COLONESE, P. H.; ARAGÃO, G. B.; DIORIO, T. A. A Matemática no Espaço Ciência Viva: Aventuras Geométricas in  ESPAÇO CIÊNCIA VIVA (Org.) Caderno de Mediação 2011, 1 edição, Rio de Janeiro, Espaço Ciência Viva, 2011.
• GÊNOVA, A. C.; Brincando com Tangram em Origami, Editora Global, 3ª Edição, Rio de Janeiro, ISBN: 9788526002470; ISBN-10: 8526002473.
• KOZMINSKI, E. L., As três partes. Coleção Lagarta Pintada. Editora Ática, 2009, 12ª edição, ISBN-13: 9788508125852.
• TEIXEIRA, M. R. Uma história da China. Coleção: Matemática em mil e uma histórias. Editora FTD, 1998. ISBN: 8532235913.